Một số được gọi là số đối xứng đặc biệt nếu nó là một số đối xứng và có độ dài chẵn

Yêu cầu: Tìm số đối xứng đặc biệt thứ ~n~

Input

1 dòng duy nhất là số nguyên n

Output

Yêu cầu của bài toán

Giới hạn

• ~n \le 10^{100000}~

Ví dụ

Sample input

10

Sample output

1001

Giải thích ví dụ

~11, 22, 33, 44, 55, 66, 77, 88, 99, 1001~

Cho một hình có quy luật như sau:

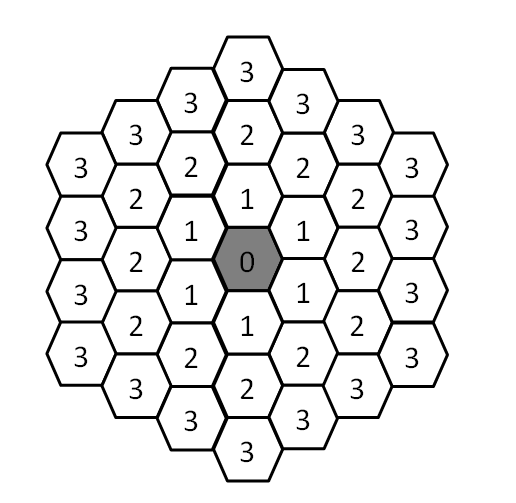
Các ô ở vòng ngoài có giá trị lớn hơn ô ở vòng trong ~1~ đơn vị

Yêu cầu: Đếm số ô có giá trị nhỏ hơn hoặc bằng ~n~

Input

~1~ dòng duy nhất là số nguyên ~n~

Output

~1~ dòng là số ô có giá trị nhỏ hơn hoặc bằng ~n~

Giới hạn

• ~n \le 10^9~

Ví dụ

Sample input

2

Sample output

19

Một số được gọi là số xinh đẹp nếu các chữ số của nó nằm trong tập ~{1, 3, 0, 2}~

Yêu cầu: Đếm số lượng số xinh đẹp có số chữ số bằng ~n~

Input

~1~ dòng duy nhất là số nguyên ~n~

Output

Yêu cầu của bài toán (Phần dư khi chia cho ~10^9 + 7~)

Giới hạn

• ~2/16~ test có ~n \le 20~
• ~10/16~ test có ~n \le 10^5~
• ~4/16~ test có ~n \le 10^{15}~

Ví dụ

Sample input

2

Sample output

12

Giải thích ví dụ

~12~ số xinh đẹp có số chữ số bằng ~2~ : ~10, 11, 12, 13, 20, 21, 22, 23, 30, 31, 32, 33~

Cho một số nguyên dương ~n~. Ở mỗi bước, bạn có thể lấy ~n~ trừ cho 1 trong các chữ số của ~n~

Yêu cầu: Số bước ít nhất để ~n~ bằng 0

Input

1 dòng duy nhất là số nguyên dương n

Output

Yêu cầu của bài toán

Giới hạn

• ~4/13~ test có ~n \le 10^3~
• ~n \le 10^6~

Ví dụ

Sample input

27

Sample output

5

Giải thích ví dụ

~27 -> 20 -> 18 -> 10 -> 9 -> 0~

Trường THCS Huỳnh Bá Chánh có ~N~ học sinh ~(N \le 10^5)~, học sinh thứ ~i~ đến trường vào thời diểm ~a[i]~ và ra về vào thời điểm ~b[i]~ ~(0 \le a[i] \le b[i] \le 10^9)~.

Yêu cầu: Tìm số lượng học sinh nhiều nhất có mặt ở trường vào một thời điểm bất kì.

Input

Dòng đầu tiên là số nguyên ~N~ là số lượng học sinh đến trường.

~N~ dòng tiếp theo, mỗi dòng là ~2~ số nguyên ~a[i], b[i] (a[i] \le b[i] \le 10^9)~ lần lượt là thời điểm đến trường và ra về của học sinh thứ ~i~.

Output

Yêu cầu của bài toán

Giới hạn

• ~40~% số điểm có ~N * max(b[i]) \le 10^6~.
• ~60~% số điểm có ~N \le 10^5~ và ~a[i], b[i] \le 10^9~.

Ví dụ

Sample input

4
1 3
2 4
5 6
6 7

Sample output

2

Giải thích ví dụ

dễ thấy có nhiều nhất ~2~ người ở các thời điểm ~2, 3, 6~ (Lưu ý chỉ in ra số người nhiều nhất trong thời điểm đó)

Cho ~N~ điểm trong mặt phẳng toạ độ ~Oxy~, điểm thứ i có toạ độ nguyên ~(x_i ; y_i)~. Ta định nghĩa khoảng cách Manhattan giữa hai điểm ~i,j~ là ~|x_i - x_j| +|y_i - y_j|~.

Yêu cầu: Hãy tính tổng khoảng cách Manhattan giữa mọi cặp điểm.

Input

• Dòng đầu tiên là số ~N~ ~(1 \le N \le 10^5)~, số cặp điểm
• ~N~ dòng sau, dòng thứ ~i~ ghi cặp số nguyên ~(x_i, y_i)~ ~(-10^9 \le x_i, y_i \le 10^9)~ là toạ độ điểm thứ ~i~ trên mặt phẳng

Output

In ra tổng khoảng cách Manhattan giữa mọi cặp điểm

Giới hạn

• Subtask 1: ~25~% test có ~𝑁 ≤ 10^3~
• Subtask 2: ~75~% test có ~𝑁 ≤ 10^5~

Ví dụ

Sample input

3
1 1
1 2
3 3

Sample output

8

Giải thích ví dụ

• Tự đếm