Tìm kiếm nhị phân (Chặt nhị phân) là một giải pháp tìm kiếm nhanh trên một dãy số đã được sắp xếp theo thứ tự không giảm (hoặc không tăng)
Ý tưởng của giải pháp là xác định vị trí trung vị của không gian tìm kiếm sau đó đối chiếu với kết quả cần tìm từ đó tiếp tục xác định không gian tìm kiếm tiếp theo hoặc đưa ra kết quả (tìm thấy hoặc không tìm thấy)
Giải thích cách hoạt động:
Bước 1: Khởi tạo hai biến $left$ và $right$ là chỉ số đầu và cuối của mảng.
Bước 2: lặp lại các thao tác sau khi $left$ không vượt qua $right$, thực hiện các bước sau:
- Xác định vị trí trung vị ($mid$) bằng công thức ($left$ + $right$) div 2.
- So sánh giá trị tại vị trí trung vị($mid$) với giá trị cần tìm.
- Nếu giá trị tại $mid$ bằng giá trị cần tìm, trả về chỉ số $mid$. Kết thúc
- Nếu giá trị tại $mid$ nhỏ hơn giá trị cần tìm, thì tìm kiếm ở nửa phải của mảng.
- Ngược lại, tìm kiếm ở nửa trái của mảng.
Bước 3: Trả về kết quả không tìm thấy. Kết thúc
Thuật toán tìm kiếm nhị phân có độ phức tạp thời gian là $O(logN)$, nơi N là số lượng phần tử trong mảng, giúp nó trở thành một trong những thuật toán tìm kiếm hiệu quả nhất khi mảng đã được sắp xếp.
Mô phỏng thực thi thuật toán với mảng A=[0,5,13,19,2,41,55,68,72,81,98] và x=55, thuật toán sẽ diễn ra như hình sau đây: 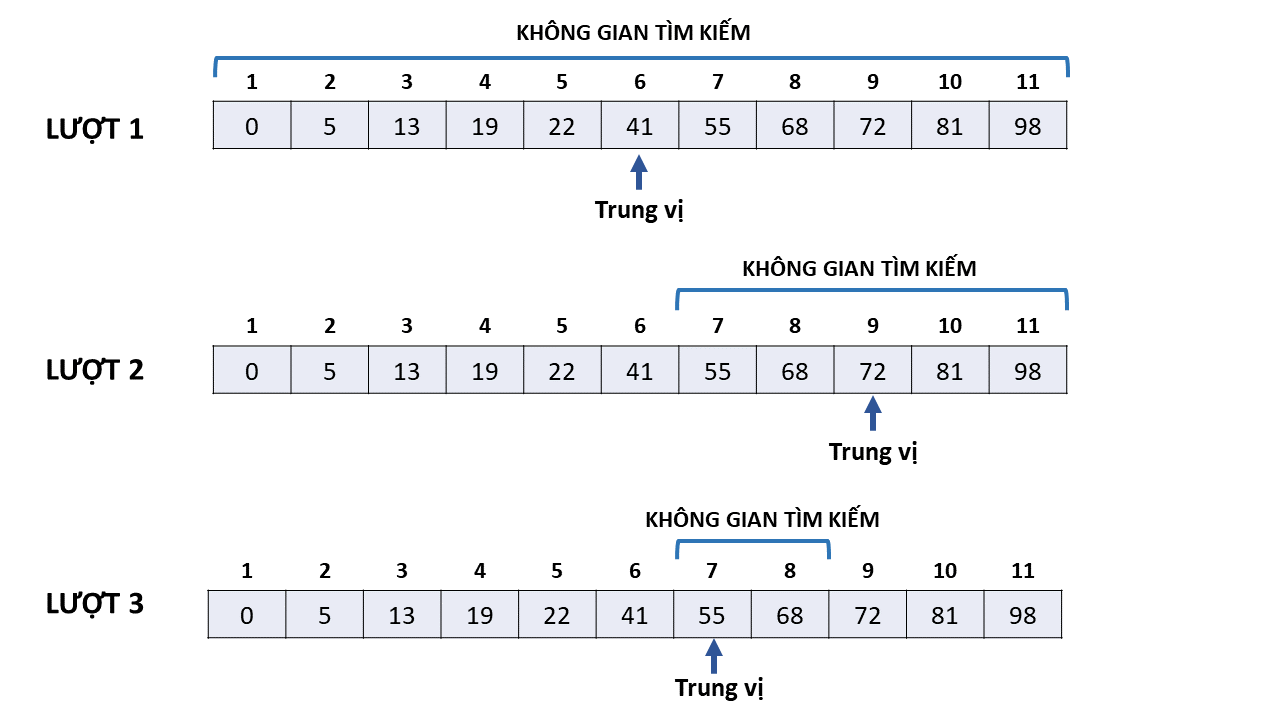Lượt 1:
+ Không gian tìm kiếm là cả mảng $A$
+ Vị trí trung vị mid = (1 + 11) div 2 = 6
+ $A$ ₆ = 41 < x = 55 do đó thay đổi không gian tìm kiếm từ vị trí 7 (tức là $mid$ + 1) đến vị trí 11. Ở đây nếu $mid$ > $x$ thì không gian tìm kiếm sẽ thay đổi thành từ vị trí 1 đến vị trí 5(tức là $mid$ - 1)
Lượt 2:
+ Không gian tìm kiếm là từ vị trí 7 đến vị trí 11
+ Vị trí trung vị mid = (7 + 11) div 2 = 9
+ $A$ ₉ = 72 > x = 55 do đó không gian tìm kiếm từ vị trí 7 đến vị trí 8
Lượt 3:
+ Không gian tìm kiếm là từ vị trí 7 đến vị trí 8
+ Vị trí trung vị mid = (7 + 8) div 2 = 7
+ $A$ ₇ = x = 55 vậy kết luận vị trí bằng 55 chính là $mid$ = 7
Các hàm tìm kiếm nhị phân trong c++

// chương trình
#include <bits/stdc++.h>

int main() {
const int size = 10;
int arr[size] = {1, 2, 2, 4, 4, 4, 7, 8, 9, 10};
int target = 4;

// Sắp xếp mảng trước khi sử dụng lower_bound và upper_bound
std::sort(arr, arr + size);

// lower_bound: iterator đến phần tử đầu tiên không nhỏ hơn giá trị cần tìm
auto lower_bound_iter = std::lower_bound(arr, arr + size, target);

// upper_bound: iterator đến phần tử đầu tiên lớn hơn giá trị cần tìm
auto upper_bound_iter = std::upper_bound(arr, arr + size, target);

// binary_search: kiểm tra xem giá trị có tồn tại trong mảng hay không
bool found = std::binary_search(arr, arr + size, target);

// equal_range: trả về một cặp iterator là lower_bound và upper_bound
auto equal_range_pair = std::equal_range(arr, arr + size, target);

// Hiển thị kết quả
if (found) {
    std::cout << "Phan tu " << target << " duoc tim thay.\n";
} else {
    std::cout << "Phan tu " << target << " khong tim thay.\n";
}

// Hiển thị phần tử đầu tiên không nhỏ hơn giá trị cần tìm
std::cout << "Lower Bound: " << *lower_bound_iter << " at index " << std::distance(arr, lower_bound_iter) << std::endl;

// Hiển thị phần tử đầu tiên lớn hơn giá trị cần tìm
std::cout << "Upper Bound: " << *upper_bound_iter << " at index " << std::distance(arr, upper_bound_iter) << std::endl;

// Hiển thị equal_range
std::cout << "Equal Range: [" << *equal_range_pair.first << ", " << *equal_range_pair.second << ")\n";

return 0;
}